Coordinate Tetra Spaziali

Sistema di coordinate spaziali basati su geometria tetraedrica

Stiamo vivendo in un periodo di accettazione pressoché totale del sistema cartesiano di coordinate spaziali, il quale si basa su tre assi coordinati in angolazioni di 90 gradi. Perciò potrebbe sembrare suicidio intellettuale, o perlomeno cosa rischiosa e molto eccentrica, parlare di un diverso sistema di coordinate spaziali ed asserire che questo sistema alternativo potrebbe avere considerevoli vantaggi. Ciò nonostante, un sistema alternativo è stato scoperto ed è disponibile per essere studiato, approfondito ed usato.

Si celebra quest'anno il quattrocentesimo anniversario della nascita di Cartesio per ricordare i suoi notevoli contributi allo sviluppo della scienza e della filosofia, avendo introdotto il ragionamento scientifico laddove prima regnava sovrana l'autorità pura ed arbitraria. Tratteremo qui solamente una delle sue scoperte, quella di un sistema razionale di coordinate spaziali, il quale ci permette di determinare la precisa posizione di qualsiasi oggetto che stia dentro uno spazio conosciuto.
Si dice che Cartesio abbia inventato questo sistema di coordinate osservando le curve irregolari del volo di una mosca nella sua stanza rendendosi conto che se avesse potuto misurare la distanza da ognuno degli assi che partivano da un angolo della stanza, avrebbe potuto essere certo della posizione della mosca nello spazio in qualsiasi momento. Una serie di posizioni così definite avrebbe naturalmente permesso di definire con certezza matematica le curve meandriche che l'insetto tracciava. Naturalmente non possiamo essere certi che la scoperta sia avvenuta proprio così, ma una cosa possiamo presumere con certezza: il sistema cartesiano di coordinate si basa essenzialmente sulla geometria delle costruzioni civili preferita ancora oggi, cioè la configurazione rettangolare della maggior parte delle case e delle loro stanze interne.

Buckminster Fuller, d'altro canto, ha vissuto molto più vicino al nostro tempo che non Cartesio. Fuller morì nel 1983 all'età di 87 anni. Come Cartesio, Fuller ha contribuito molto allo sviluppo della scienza e della filosofia. Probabilmente la cosa per la quale lo ricordiamo di più è la sua scoperta del metodo di costruzione detto geodesico, cioè la costruzione di strutture tondeggianti, costituite esclusivamente di elementi portanti connessi in forma triangolare. Ma anche dopo la sua morte è avvenuta una importante conferma delle sue teorie geometriche con la scoperta della straordinaria molecola sferica di carbone 60, chiamata Buckminsterfullerene, avvenuta pochi anni or sono.

La geometria di Fuller è stata nominata Sinergetica ed è stata sviluppata dall'osservazione sperimentale del comportamento di sfere di uguale diametro, sistemate l'una vicino all'altra il più possibile, e così formando delle figure geometriche. La più semplice ed al contempo più importante configurazione stabile così ottenuta è il tetraedro, che è il risultato di quattro sfere che, toccandosi a vicenda, formano una configurazione perfettamente triangolare, un tetraedro appunto, composto di quattro angoli di 60 gradi (fig. 1). Altri elementi importanti sono l'ottaedro (formato da sei sfere adiacenti) ed il cosiddetto vector equilibrium (equilibrio di vettori) che è il risultato di dodici sfere che si associano ad una tredicesima sfera centrale in configurazione compatta, coordinata sempre ad angolazioni di 60 gradi.

Il cubo, che forma la base dei nostri odierni metodi di costruzione abitativa e del sistema cartesiano di coordinate x-y-z, non è di per sé una configurazione stabile. Le otto sfere che formano un cubo sono instabili, a meno che non vengano connesse come le sfere che formano il tetraedro. In questo modo, due tetraedri interconnessi ai rispettivi centri, formano un cubo di otto sfere.

Sembra che la geometria dimostrata dalle teorie di Fuller ci permetta di spiegare per esempio le varie forme dei cristalli, così come la configurazione delle molecole e perfino dei virus. La sua applicazione nell'ingegneria ci da la possibilità di formare delle strutture molto efficienti in termini di economia delle materie prime e di resistenza delle costruzioni stesse.
Come si potrebbero utilizzare le scoperte di Fuller per l'ideazione di un sistema di coordinate e soprattutto, perché si dovrebbe affrontare un simile lavoro, visto che il sistema cartesiano ci ha soddisfatto perfettamente (o quasi) per lungo tempo?

Prima di tutto, le coordinate cartesiane sono sì una comoda astrazione matematica, ma non sono in accordo con le strutturazioni naturali, così come l'odierna chimica non riuscirà mai a copiare con esattezza le funzioni biologiche di un organismo vivente.
Se si vogliono utilizzare le coordinate cartesiane per l'orientamento nello spazio illimitato, e non in uno spazio definito come fece Cartesio, se cioè, i nostri tre assi devono formare il punto di origine di un sistema aperto in tutte le direzioni, non ci sono più sufficienti. Dobbiamo raddoppiare il sistema, aggiungendo altri tre assi (un immagine a specchio dei primi tre), in modo che diventi possibile descrivere lo spazio "dietro l'angolo" (fig. 2).

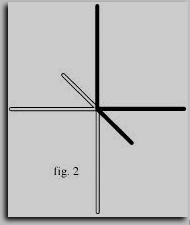Normalmente non abbiamo l'impressione di un raddoppio degli assi, perché diamo semplicemente dei valori negativi ad una direzione dell'asse e dei valori positivi a quella opposta. Il fatto che la parte negativa e quella positiva di ogni asse sembrino il loro reciproco prolungamento, non giustifica però di considerarli come un'asse unico. Rigorosamente dobbiamo considerare sei assi: l'asse x positivo e l'asse x negativo, l'y positivo e l'y negativo ed infine lo z positivo e quello negativo. Infatti, se ci vogliamo orientare, dobbiamo specificare se stiamo parlando di un punto in relazione all'asse positivo o a quello negativo, anche se lo facciamo semplicemente considerando i numeri positivi come appartenenti all'asse positivo e quelli negativi all'asse negativo. Quindi, per determinare un punto nello spazio lo definiamo in relazione a tre da un totale di sei assi.

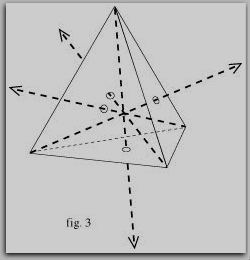
Questo è il punto dove la geometria sinergetica di Fuller ci offre una possibilità di semplificare di molto il nostro compito. Se decidiamo di ridurre il numero degli assi da sei a quattro, prendendo come punto di partenza la figura geometrica più semplice e basilare, il tetraedro, diventa possibile definire l'esatta posizione di un punto nello spazio con riferimento a tre da un totale di quattro (invece di sei) assi. I quattro assi di questo sistema di coordinate sono gli assi che hanno origine da ognuno dei vertici del tetraedro, incontrandosi nel suo punto centrale ed uscendo perpendicolarmente alla superficie triangolare opposta (fig.3). Questi assi formano tra di loro angoli di 109 gradi, 28 minuti e rappresentano il numero minimo di assi convergenti in un unico punto, necessari per poter definire tutte le possibili direzioni nello spazio.
L'autore ha sviluppato un sistema di codifica a colori il quale combina le coordinate spaziali tetraedriche con il metodo di separazione dei colori usato oggi nella stampa di qualsiasi immagine colorata, detto CMYK, a dimostrazione di questo concetto e così da permettere la sua applicazione per l'orientamento intuitivo ed istantaneo nello spazio.

I colori CMYK (ciano, magenta, giallo [yellow] e nero [black]) sono i quattro colori base che si usano nei processi di stampa tipografica. La loro sovrapposizione in diverse percentuali crea un grande numero di colori diversi in tonalità quasi infinite. Assegniamo uno dei colori base ad ognuno dei quattro assi. Da un'intensità del 100 % in vicinanza dell'asse vengono sfumati in modo uniforme ed in decrescente intensità fino ad arrivare agli altri assi. In questo modo otteniamo un colore diverso per ognuna delle migliaia o addirittura milioni di possibili direzioni che vorremmo identificare. Resta naturalmente ferma la possibilità di esprimere la direzione in termini di gradi, minuti e secondi d'arco in relazione a tre degli assi.

Un sistema di coordinate basato sui principi qui esposti, approfondito e sviluppato nei dettagli, può essere utile nell'astronomia, nella navigazione (specialmente quella spaziale), nella rappresentazione olografica delle immagini, nell'immagazzinamento elettronico di dati ed informazioni nei cristalli e probabilmente in tutta una serie di altre attività ancora da ideare.

Usando questo sistema, trasformeremo le nostre quattro direzioni di orientamento sulla terra (est-ovest-nord-sud) in quattro direzioni per l'orientamento nello spazio. Bisogna sviluppare ed usare questo strumento se stiamo considerando seriamente di espandere la nostra influenza nello spazio interplanetario o interstellare, non solo con osservazioni sempre più accurate ma anche con l'esplorazione e la navigazione.

Un commento ancora sul concetto di "dimensione", che sembra non sia stato sviluppato con sufficiente chiarezza dalla scienza odierna.

Siamo soliti chiamare il nostro universo fisico un universo tridimensionale. I libri di testo e le enciclopedie ci dicono che lo spazio ha tre dimensioni, senza considerare che il numero di dimensioni che assegniamo allo spazio dipende solamente dal riferimento geometrico che usiamo. In un primo momento, dopo aver scritto questo articolo mi è venuto spontaneo dire che ovviamente, considerando le coordinate spaziali tetraedriche, lo spazio deve avere quattro dimensioni. Ma questo sarebbe fare lo stesso sbaglio degli autoritari insegnamenti odierni.

Infatti lo spazio ha solamente una "dimensione" che possiamo anche chiamare "estensione". Non importa a quante direzioni vogliamo far riferimento nel nostro sistema di orientamento, siano esse tre, quattro o forse dieci. Stiamo sempre e comunque considerando lo stesso spazio. Il termine 'tridimensionale' ha assai poca rilevanza fisica come lo avrebbero i termini 'quadridimensionale' oppure 'n-dimensionale'. Il concetto di "dimensione" quindi, non è altro che un modo di interpretare matematicamente la realtà fisica che chiamiamo spazio.

Josef Hasslberger
3 febbraio 1996

Riferimenti:
  1. Fuller, R. Buckminster "Synergetics", 1982, Macmillan Publishing Company, 866 Third Avenue, New York, N.Y. 10022
  2. Fuller, R. Buckminster "Cosmography", 1991, Macmillan Publishing Company
L'indirizzo del autore è:
Rampa Brancaleone 25, 00165 Roma - Italia. Telefono (6) 635884 fax (6) 632196
(e-mail: sepp@lastrega.com)


Per informazioni su Buckminster Fuller ed i suoi lavori scientifici:
Buckminster Fuller Institute, 1743 South La Cienega Blvd.,
Los Angeles, CA 90035 Telephone (213) 837 7710


Due pagine web interessanti sono:
http://www.grunch.net/synergetics/quadintro.html
http://www.grunch.net/synergetics/quadcolors.html